Introduction to Data Science

Getting Data and Simpson’s Paradox

Author

Joanna Bieri
DATA101

Important Information

Email: joanna_bieri@redlands.edu
Office Hours: Duke 209 Click Here for Joanna’s Schedule

Announcements

In NEXT WEEK - Data Ethics This week you should be reading your book or articles.

Day 11 Assignment - same drill.

Make sure Pull any new content from the class repo - then Copy it over into your working diretory.
Open the file Day##-HW.ipynb and start doing the problems.
- You can do these problems as you follow along with the lecture notes and video.
Get as far as you can before class.
Submit what you have so far Commit and Push to Git.
Take the daily check in quiz on Canvas.
Come to class with lots of questions!

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import plotly.express as px
from plotly.subplots import make_subplots
import plotly.io as pio
pio.renderers.defaule = 'colab'

from itables import show

# This stops a few warning messages from showing
pd.options.mode.chained_assignment = None 
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)

————————

Where does data come from?

Scientific Studies
User Data
Geographic or Spatial Data

Today we will focus on Scientific Studies - when data is intentionally gathered to better understand a specific problem.

This lab follows the Data Science in a Box units “Scientific Studies, Simpsons Paradox and Doing Data Science” by Mine Çetinkaya-Rundel. It has been updated for our class and translated to Python by Joanna Bieri.

Two types of Scientific Studies

Observational Data Data collected so that collection does not interfere with how the data arise. The goal is to establish associations. Cannot find causation.
Experimental Data Randomly assign treatment groups, gather data from those groups. The goal is to establish causal connections.

————————

Case Studies

What type of Study:

What type of study is the following, observational or experiment? What does that mean in terms of causal conclusions?

Researchers studying the relationship between exercising and energy levels asked participants in their study how many times a week they exercise and whether they have high or low energy when they wake up in the morning.

Based on responses to the exercise question the researchers grouped people into three categories (no exercise, exercise 1-3 times a week, and exercise more than 3 times a week).

The researchers then compared the proportions of people who said they have high energy in the mornings across the three exercise categories.

Answer

This is an observational study. Even though they broke the people into categories, they did not assign people to different treatments. The best we can do is see an association.

We could say in our study people who exercised had higher energy.

We cannot say that exercising causes people to have more energy.

What type of Study:

What type of study is the following, observational or experiment? What does that mean in terms of causal conclusions?

Researchers studying the relationship between exercising and energy levels randomly assigned participants in their study into three groups: no exercise, exercise 1-3 times a week, and exercise more than 3 times a week.

After one week, participants were asked whether they have high or low energy when they wake up in the morning.

The researchers then compared the proportions of people who said they have high energy in the mornings across the three exercise categories.

Answer

This is an experimental study because they assigned different treatments, assuming everything else is the same. If we saw the same results as the previous study then in this case we can say that exercise caused higher energy.

What type of Study:

Girls who ate breakfast of any type had a lower average body mass index (BMI), a common obesity gauge, than those who said they didn’t. The index was even lower for girls who said they ate cereal for breakfast, according to findings of the study conducted by the Maryland Medical Research Institute with funding from the National Institutes of Health (NIH) and cereal-maker General Mills. […]

The results were gleaned from a larger NIH survey of 2,379 girls in California, Ohio, and Maryland who were tracked between the ages of 9 and 19. […]

As part of the survey, the girls were asked once a year what they had eaten during the previous three days.* […]

Souce: Study: Cereal Keeps Girls Slim, Retrieved Sep 13, 2018.

Explanatory Variable

Whether the participant ate breakfast of not

Response Variable

BMI of the participant

Possible Explanations

Eating breakfast causes girls to be slimmer
Being slim causes girls to eat breakfast
A third variable is responsible for both – a confounding variable: an extraneous variable that affects both the explanatory and the response variable, and that makes it seem like there is a relationship between them

Answer

This is a causal study. The followed the participants over years, but did not assign them to study groups. We cannot find causation. It would be easy for a third variable to be confounding the results (sleep, family traditions, etc)

————————

So what does this mean about my data?

We want to be very careful about what we deduce from study data. Know what kind of study was done when reporting your results!

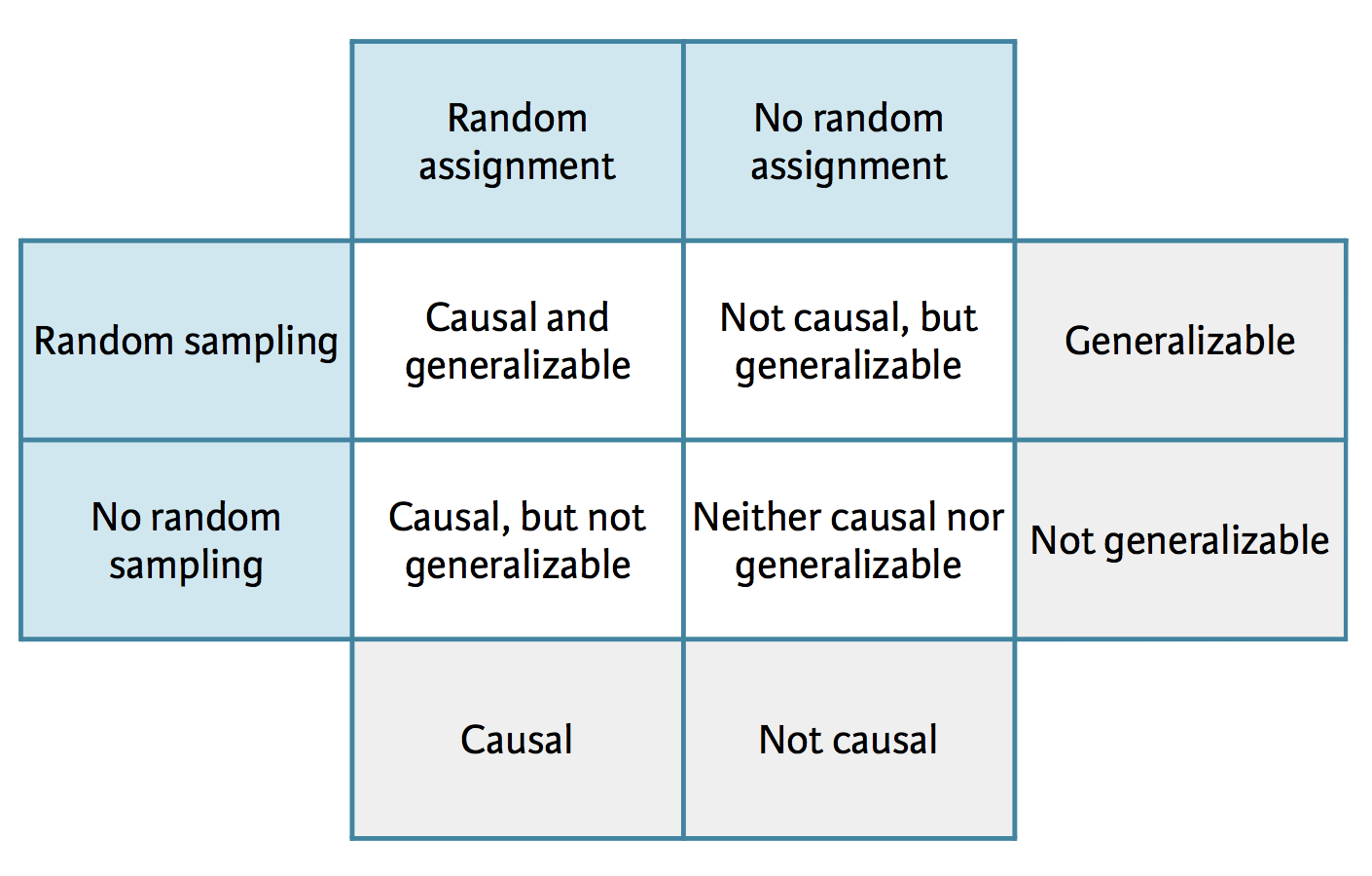
Image thanks to Data Science in a Box

Random Assignment means studies assign participants to treatment groups randomly

Random Sampling means that you randomly sample the population at large (very hard to do)

Generalizable means that your study should apply to the general population

Example - Climate Change

A July 2019 YouGov survey asked 1633 GB and 1333 USA randomly selected adults which of the following statements about the global environment best describes their view:

They had the choices:

The climate is changing and human activity is mainly responsible
The climate is changing and human activity is partly responsible, together with other factors
The climate is changing but human activity is not responsible at all
The climate is not changing

Source: YouGov - International Climate Change Survey

What kind of study is this?

What kind of results can we find?

Answer

This is a causal study. We can find associations.

Here is the data

Here we specify index_col=0 this makes it so instead of numbers on the far left we have the country abbreviations, which were in the first column of the .csv file.

file_name = 'data/yougov-climate.csv'
DF = pd.read_csv(file_name,index_col=0)
DF

	The climate is changing and human activity is mainly responsible	The climate is changing and human activity is partly responsible, together with other factors	The climate is changing but human activity is not responsible at all	The climate is not changing	Don't know
country
GB	833	604	49	33	114
US	507	493	120	80	133

First question:

What percent of all respondents think the climate is changing and human activity is mainly responsible?

Get totals across rows and columns:

The .sum() command can sum the rows (axis=0) or the columns (axis=1) of a data frame.

DF.loc['total']= DF.sum(axis=0)
DF['total'] = DF.sum(axis=1)
DF

	The climate is changing and human activity is mainly responsible	The climate is changing and human activity is partly responsible, together with other factors	The climate is changing but human activity is not responsible at all	The climate is not changing	Don't know	total
country
GB	833	604	49	33	114	1633
US	507	493	120	80	133	1333
total	2680	2194	338	226	494	5932

Percent is just the part divided by the total. So we need to:

Find the total number of survey respondents.
Find the total number of survey respondents who thought human activity is responsible.
Divide those two numbers to get a decimal

all_respondents = DF['total'].loc['total']
human_responsible = DF['The climate is changing and human activity is mainly responsible  ']['total']
human_responsible/all_respondents

0.45178691840863117

This means that overall 45.2% of people think that climate is changing and human activity is mainly responsible.

Second question:

What percent of GB respondents think the climate is changing and human activity is mainly responsible?

gb_respondants = DF['total'].loc['GB']
GB_human_responsible = DF['The climate is changing and human activity is mainly responsible  ']['GB']
GB_human_responsible/gb_respondants

0.5101041028781383

Of the people would responded from Great Britain, 51% think that climate is changing and human activity is mainly responsible.

Third Question

What percent of US respondents think the climate is changing and
human activity is mainly responsible?

us_respondants = DF['total'].loc['US']
US_human_responsible = DF['The climate is changing and human activity is mainly responsible  ']['US']
US_human_responsible/us_respondants

0.3803450862715679

When we consider US respondents we see that 38% (lower than GB) believe that climate is changing and human activity is mainly responsible.

What can we say?

Based on the percentages we calculated, does there appear to be a relationship between country and beliefs about climate change? If yes, could there be another variable that explains this relationship?

There is a clear difference between Great Britain and the USA.
So there is an association between country and your answer to this question.
Could there be other confounding variables? YES!

We cannot say that being from GB causes you to be more likely to believe climate changes is caused by human activity. We can only say that there is a relationship between country and your belief.

————————

Conditional Probability

What do these percentages represent? We can say:

If you are from the US there is a 38% probability that you believe climate change is caused by human activity.
If you are from the GB there is a 51% probability that you believe climate change is caused by human activity.

This is called Conditional Probability $ P(A|B):$ Probability of event A given event B

Example: two different questions:

What is the probability that it will be unseasonably warm tomorrow?
What is the probability that it will be unseasonably warm tomorrow given that it was unseasonably warm today?

Independence

If knowing event A happened tells you something about event B happening - then these two things are linked - and we say A and B are not independent.

In our example: If you found that a person believed that climate change was not caused by human activity, it is more likely that they are from the US. Because these two things are not independent.

Otherwise events A and B are said to be independent and we know $P(A|B) = P(A)$ - because knowing B doesn’t tell you anything about A.

Q Repeat the analysis for one of the other columns/questions.

Percent total
Percent from GB
Percent from US

Talk about the conditional probability in this case:

eg. In a person is from ________ then there is a ________ probability that they believe _______. If a person answered _______ then they are more likley to be from ________.

————————

Simpson’s Paradox

Berkeley admission data example

Study carried out by the Graduate Division of the University of California, Berkeley in the early 70’s to evaluate whether there was a gender bias in graduate admissions.
The data come from six departments. For confidentiality we’ll call them A-F.
We have information on whether the applicant was male or female and whether they were admitted or rejected. This is an old study so only two binary classifications were used.

Here is the data

file_name = 'data/berkley.csv'
DF = pd.read_csv(file_name)
show(DF)

Department	Male Yes	Male No	Female Yes	Female No
Loading ITables v2.1.4 from the internet... (need help?)

DF_melt = pd.melt(DF,id_vars=['Department'],var_name='MF',value_name='Number')
DF_melt

	Department	MF	Number
0	A	Male Yes	512
1	B	Male Yes	353
2	C	Male Yes	120
3	D	Male Yes	138
4	E	Male Yes	53
5	F	Male Yes	22
6	A	Male No	313
7	B	Male No	207
8	C	Male No	205
9	D	Male No	279
10	E	Male No	138
11	F	Male No	351
12	A	Female Yes	89
13	B	Female Yes	17
14	C	Female Yes	202
15	D	Female Yes	131
16	E	Female Yes	94
17	F	Female Yes	24
18	A	Female No	19
19	B	Female No	8
20	C	Female No	391
21	D	Female No	244
22	E	Female No	299
23	F	Female No	317

DF_melt['gender'] = DF_melt['MF'].apply(lambda x: x.split(' ')[0]).copy()
DF_melt['admitted'] = DF_melt['MF'].apply(lambda x: x.split(' ')[1]).copy()

DF_melt

	Department	MF	Number	gender	admitted
0	A	Male Yes	512	Male	Yes
1	B	Male Yes	353	Male	Yes
2	C	Male Yes	120	Male	Yes
3	D	Male Yes	138	Male	Yes
4	E	Male Yes	53	Male	Yes
5	F	Male Yes	22	Male	Yes
6	A	Male No	313	Male	No
7	B	Male No	207	Male	No
8	C	Male No	205	Male	No
9	D	Male No	279	Male	No
10	E	Male No	138	Male	No
11	F	Male No	351	Male	No
12	A	Female Yes	89	Female	Yes
13	B	Female Yes	17	Female	Yes
14	C	Female Yes	202	Female	Yes
15	D	Female Yes	131	Female	Yes
16	E	Female Yes	94	Female	Yes
17	F	Female Yes	24	Female	Yes
18	A	Female No	19	Female	No
19	B	Female No	8	Female	No
20	C	Female No	391	Female	No
21	D	Female No	244	Female	No
22	E	Female No	299	Female	No
23	F	Female No	317	Female	No

Percent males vs females

First, we will evaluate whether the percentage of males admitted is indeed higher than females, overall.

\[ P(Admit | Male) \]

\[ P(Admit | Female) \]

my_columns = ['Number','gender','admitted']
DF_totals = DF_melt[my_columns].groupby(['gender','admitted'],as_index=False).sum()
DF_totals

	gender	admitted	Number
0	Female	No	1278
1	Female	Yes	557
2	Male	No	1493
3	Male	Yes	1198

# Get the total numbers in each group
mask = DF_totals['gender'] == 'Male'
num_male = DF_totals[mask]['Number'].sum()
mask = DF_totals['gender'] == 'Female'
num_female = DF_totals[mask]['Number'].sum()

# # Find the percents
mask = (DF_totals['gender'] == 'Male') & (DF_totals['admitted'] == 'Yes')
prob_male = DF_totals[mask]['Number']/num_male
mask = (DF_totals['gender'] == 'Female') & (DF_totals['admitted'] == 'Yes')
prob_female = DF_totals[mask]['Number']/num_female

prob_male

3    0.445188
Name: Number, dtype: float64

prob_female

1    0.303542
Name: Number, dtype: float64

So mathematically we can say:

\[ P(Admit | Male) = 0.445\]

\[ P(Admit | Female) = 0.304\]

So the answer is YES the admission rate is higer for males.

fig = px.histogram(DF_totals,
                     x='Number',
                     y='gender',
                     color='admitted',
                     barnorm = "percent",
                     color_discrete_map = {'No':'#99d8c9','Yes':'#2ca25f'})

fig.update_layout(title='Percent male and female applications',
                  title_x=0.5,
                  template="plotly_white",
                  xaxis_title="",
                  yaxis_title="Gender",
                  legend_title='Admitted',
                  autosize=False,
                  width=800,
                  height=500)

fig.show()

What do we see here?

Well it does in fact look like women were admitted at a lower rate than men.

Another way to do this - multi index data frame

If you us .groupby() with more than one column and don’t specify as_index=False then you get a multi index data frame. This can be really convenient. Below is our calculation using the multi index data frame.

WARNING Plotly express will give errors if you try to send it a multi index data frame.

my_columns = ['Number','gender','admitted']
DF_totals = DF_melt[my_columns].groupby(['gender','admitted']).sum()
DF_totals

		Number
gender	admitted
Female	No	1278
Female	Yes	557
Male	No	1493
Male	Yes	1198

# Get the total numbers in each group
num_male = DF_totals.loc['Male'].sum()
num_female = DF_totals.loc['Female'].sum()

# # Find the percents
prob_male = DF_totals.loc['Male','Yes']/num_male
prob_female = DF_totals.loc['Female', 'Yes']/num_female

print(prob_male)
print(prob_female)

Number    0.445188
dtype: float64
Number    0.303542
dtype: float64

Gender distribution by department

What can we say about the gender distribution if we look at the individual departments.

Start with our original “melted” data frame:

DF_melt

	Department	MF	Number	gender	admitted
0	A	Male Yes	512	Male	Yes
1	B	Male Yes	353	Male	Yes
2	C	Male Yes	120	Male	Yes
3	D	Male Yes	138	Male	Yes
4	E	Male Yes	53	Male	Yes
5	F	Male Yes	22	Male	Yes
6	A	Male No	313	Male	No
7	B	Male No	207	Male	No
8	C	Male No	205	Male	No
9	D	Male No	279	Male	No
10	E	Male No	138	Male	No
11	F	Male No	351	Male	No
12	A	Female Yes	89	Female	Yes
13	B	Female Yes	17	Female	Yes
14	C	Female Yes	202	Female	Yes
15	D	Female Yes	131	Female	Yes
16	E	Female Yes	94	Female	Yes
17	F	Female Yes	24	Female	Yes
18	A	Female No	19	Female	No
19	B	Female No	8	Female	No
20	C	Female No	391	Female	No
21	D	Female No	244	Female	No
22	E	Female No	299	Female	No
23	F	Female No	317	Female	No

Lets pivot!

Pivot this data so that our departments become the column labels and our MF column becomes the index.

DF_dept = DF_melt.pivot(index='MF',columns='Department',values='Number')
DF_dept

Department	A	B	C	D	E	F
MF
Female No	19	8	391	244	299	317
Female Yes	89	17	202	131	94	24
Male No	313	207	205	279	138	351
Male Yes	512	353	120	138	53	22

Percentages for department A

Here we can calculate the probability that a student is admitted and female or male for department A

Remember percent is just the part divide by the total.

NOTICE I am doing something new here!

DF_dept['A']['Female Yes']

This selects column ‘A’ and row named ‘Female Yes’. Another way to do this exact same thing is:

DF_dept['A'].loc['Female Yes']

prob_female = DF_dept['A']['Female Yes']/(DF_dept['A']['Female Yes']+DF_dept['A']['Female No'])
prob_male = DF_dept['A']['Male Yes']/(DF_dept['A']['Male Yes']+DF_dept['A']['Male No'])

prob_female

0.8240740740740741

prob_male

0.6206060606060606

So actually the probability of being admitted was BETTER for females.

Q Calculate the proportions for the other departments.

You can do this one by one or try using a FOR loop.

Here is a plot of the proportions data

fig = px.histogram(DF_melt,
                   y='gender',
                   x='Number',
                   barnorm = "percent",
                   color='admitted',
                   facet_col='Department',
                   facet_col_wrap=2,
                   color_discrete_map = {'No':'#99d8c9','Yes':'#2ca25f'})

fig.for_each_annotation(lambda a: a.update(text=a.text.split("=")[1]))
fig.update_xaxes(title_text='')

fig.update_layout(title='Percent male and female applications',
                  title_x=0.5,
                  template="plotly_white",
                  xaxis_title="",
                  yaxis_title="Gender",
                  legend_title='Admitted',
                  autosize=False,
                  width=800,
                  height=500)

fig.show()

What do we see here?

Well actually in department A women were more likely to be admitted by quite a bit, and in the other departments they were either just barely less than men or more than men. This seems to contradict what we saw in our plot above!

Which picture is the real story?!?

Take a closer look at the departments

How many women were applying in the first place?

DF

	Department	Male Yes	Male No	Female Yes	Female No
0	A	512	313	89	19
1	B	353	207	17	8
2	C	120	205	202	391
3	D	138	279	131	244
4	E	53	138	94	299
5	F	22	351	24	317

Add the totals column to the data

DF['totals'] = DF[['Male Yes', 'Male No', 'Female Yes', 'Female No']].sum(axis=1)

DF

	Department	Male Yes	Male No	Female Yes	Female No	totals
0	A	512	313	89	19	933
1	B	353	207	17	8	585
2	C	120	205	202	391	918
3	D	138	279	131	244	792
4	E	53	138	94	299	584
5	F	22	351	24	317	714

DF.columns

Index(['Department', 'Male Yes', 'Male No', 'Female Yes', 'Female No',
       'totals'],
      dtype='object')

Make separate Data Frames for Male and Female

DF_male = DF[['Department', 'Male Yes', 'Male No']].copy()
DF_female = DF[['Department', 'Female Yes', 'Female No']].copy()

Add columns to the data frames

Yes is the percent accepted

No is the percent not accepted

proportion is the proportion of applications from that department that came from that gender

DF_male['Yes'] = DF_male['Male Yes']/(DF_male['Male Yes']+DF_male['Male No'])
DF_male['No'] = DF_male['Male No']/(DF_male['Male Yes']+DF_male['Male No'])
DF_male['proportion'] = (DF_male['Male Yes']+DF_male['Male No'])/DF['totals']

DF_male

	Department	Male Yes	Male No	Yes	No	proportion
0	A	512	313	0.620606	0.379394	0.884244
1	B	353	207	0.630357	0.369643	0.957265
2	C	120	205	0.369231	0.630769	0.354031
3	D	138	279	0.330935	0.669065	0.526515
4	E	53	138	0.277487	0.722513	0.327055
5	F	22	351	0.058981	0.941019	0.522409

DF_female['Yes'] = DF_female['Female Yes']/(DF_female['Female Yes']+DF_female['Female No'])
DF_female['No'] = DF_female['Female No']/(DF_female['Female Yes']+DF_female['Female No'])
DF_female['proportion'] = (DF_female['Female Yes']+DF_female['Female No'])/DF['totals']

DF_female

	Department	Female Yes	Female No	Yes	No	proportion
0	A	89	19	0.824074	0.175926	0.115756
1	B	17	8	0.680000	0.320000	0.042735
2	C	202	391	0.340641	0.659359	0.645969
3	D	131	244	0.349333	0.650667	0.473485
4	E	94	299	0.239186	0.760814	0.672945
5	F	24	317	0.070381	0.929619	0.477591

These calculations give us a better picture! We see that the number of applications are not even.

Consider department A:

88.4% applications come from males and only 11.6% from females - this department admitted 512 males and 89 females. So even thought the acceptance rate for females was 82.4% this department still has a small overall number of females.

Consider department F:

This smaller department admitted about the same numbers of males and females and they got about the same number of applications from each gender.

This is Simpson’s Paradox

When we see a trend when we look at the data grouping one way, but the trend disappears or reverses when we look at the data another way.
Not considering an important variable when studying a relationship can result in Simpson’s paradox
Simpson’s paradox illustrates the effect that omission of an explanatory variable can have on the measure of association between another explanatory variable and a response variable
The inclusion of a third variable in the analysis can change the apparent relationship between the other two variables

————————

Example of Simposons Paradox

Consider some data, put it in a scatter plot and draw a line of best fit.

df = pd.DataFrame()
df['x'] = [2,3,4,5,6,7,8,9]
df['y'] = [4,3,2,1,11,10,9,8]
df['z'] = ['A','A','A','A','B','B','B','B']
df

	x	y	z
0	2	4	A
1	3	3	A
2	4	2	A
3	5	1	A
4	6	11	B
5	7	10	B
6	8	9	B
7	9	8	B

fig = px.scatter(df,x='x',y='y',trendline="ols")

fig.show()

But we ignored one of the variables z. If we include z we get a completely different picture. On average the data looked very different than when considering the subgroups.

fig = px.scatter(df,x='x',y='y',color='z',trendline="ols")

fig.show()

————————

Homework - Exercises

** Homework content and data from Data Science in a Box - he-05-legos.Rmd

This week we’ll do some data gymnastics to refresh and review what we learned over the past few weeks using (simulated) data from Lego sales in 2018 for a sample of customers who bought Legos in the US. This is different than the data we used on the Exam!

Data

file_name = 'data/lego-sales.csv'
DF = pd.read_csv(file_name)
DF

	first_name	last_name	age	phone_number	set_id	number	theme	subtheme	year	name	pieces	us_price	image_url	quantity
0	Kimberly	Beckstead	24	216-555-2549	24701	76062	DC Comics Super Heroes	Mighty Micros	2018	Robin vs. Bane	77.0	9.99	http://images.brickset.com/sets/images/76062-1...	1
1	Neel	Garvin	35	819-555-3189	25626	70595	Ninjago	Rise of the Villains	2018	Ultra Stealth Raider	1093.0	119.99	http://images.brickset.com/sets/images/70595-1...	1
2	Neel	Garvin	35	819-555-3189	24665	21031	Architecture	NaN	2018	Burj Khalifa	333.0	39.99	http://images.brickset.com/sets/images/21031-1...	1
3	Chelsea	Bouchard	41	NaN	24695	31048	Creator	NaN	2018	Lakeside Lodge	368.0	29.99	http://images.brickset.com/sets/images/31048-1...	1
4	Chelsea	Bouchard	41	NaN	25626	70595	Ninjago	Rise of the Villains	2018	Ultra Stealth Raider	1093.0	119.99	http://images.brickset.com/sets/images/70595-1...	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
615	Talise	Nieukirk	16	801-555-2343	24902	41556	Mixels	Series 7	2018	Tiketz	62.0	4.99	http://images.brickset.com/sets/images/41556-1...	2
616	Spencer	Morgan	28	784-555-3455	26041	41580	Mixels	Series 9	2018	Myke	63.0	4.99	NaN	2
617	Spencer	Morgan	28	784-555-3455	26060	5005051	Gear	Digital Media	2018	Friends of Heartlake City Girlz 4 Life	NaN	19.99	NaN	1
618	Amelia	Hageman	40	336-555-1950	24702	76063	DC Comics Super Heroes	Mighty Micros	2018	The Flash vs. Captain Cold	88.0	9.99	http://images.brickset.com/sets/images/76063-1...	2
619	Amelia	Hageman	40	336-555-1950	24720	10830	Duplo	NaN	2018	Minnie's Café	27.0	19.99	http://images.brickset.com/sets/images/10830-1...	4

620 rows × 14 columns

Exercises

Answer the following questions using reproducible Python code.
For each question, state your answer in a sentence, e.g. “In this sample, the first three common names of purchasers are …”.
Note that the answers to all questions are within the context of this particular sample of sales, i.e. you shouldn’t make inferences about the population of all Lego sales based on this sample.

Describe what you see in the data set (variables, observations, etc)
What are the three most common first names of purchasers?
What are the three most common themes of Lego sets purchased?
Among the most common theme of Lego sets purchased, what is the most common subtheme?
Create data frames for each of the ages in the following categories: “18 and under”, “19 - 25”, “26 - 35”, “36 - 50”, “51 and over”. HINT - use masks and create separate data frames -OR- create a new column with these categorical labels (more advanced).
Which age group has purchased the highest number of Lego sets.
Which age group has spent the most money on Legos?
Which Lego theme has made the most money for Lego? HINT: Simpler than #5, just use a groupby()
Which area code has spent the most money on Legos? In the US the area code is the first 3 digits of a phone number. HINT: You will need to split the phone number and get just the first three. You decided what to do about reporting the NaNs.
Come up with a question you want to answer using these data, and write it down. Then, create a data visualization that answers the question, and explain how your visualization answers the question.

	Department	Male Yes	Male No	Female Yes	Female No
0	A	512	313	89	19
1	B	353	207	17	8
2	C	120	205	202	391
3	D	138	279	131	244
4	E	53	138	94	299
5	F	22	351	24	317

	Department	Male Yes	Male No	Female Yes	Female No	totals
0	A	512	313	89	19	933
1	B	353	207	17	8	585
2	C	120	205	202	391	918
3	D	138	279	131	244	792
4	E	53	138	94	299	584
5	F	22	351	24	317	714

	Department	Male Yes	Male No	Female Yes	Female No
0	A	512	313	89	19
1	B	353	207	17	8
2	C	120	205	202	391
3	D	138	279	131	244
4	E	53	138	94	299
5	F	22	351	24	317

	Department	Male Yes	Male No	Female Yes	Female No	totals
0	A	512	313	89	19	933
1	B	353	207	17	8	585
2	C	120	205	202	391	918
3	D	138	279	131	244	792
4	E	53	138	94	299	584
5	F	22	351	24	317	714

	Department	Male Yes	Male No	Female Yes	Female No
0	A	512	313	89	19
1	B	353	207	17	8
2	C	120	205	202	391
3	D	138	279	131	244
4	E	53	138	94	299
5	F	22	351	24	317

	Department	Male Yes	Male No	Female Yes	Female No	totals
0	A	512	313	89	19	933
1	B	353	207	17	8	585
2	C	120	205	202	391	918
3	D	138	279	131	244	792
4	E	53	138	94	299	584
5	F	22	351	24	317	714