Math for Data Science

Exam Review - Linear Algebra

Author

Joanna Bieri
DATA100

Important Information

Today’s Goals:

  • Review topics from Probability for our Exam
# We will just go ahead and import all the useful packages first.
import numpy as np
import sympy as sp
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Special Functions 
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from scipy.stats import binom, beta, norm

# Functions to deal with dates
import datetime

Part 1

Matrix Computations:

Given the following definitions, complete each of the matrix computations:

\[a = 2,\;\;\; b=\frac{1}{4}, \;\;\; \vec{v}_1=\begin{bmatrix}1 \\ 1\end{bmatrix}, \;\;\;\vec{v}_2=\begin{bmatrix}2 \\ -2\end{bmatrix},\;\;\;\vec{v}_3=\begin{bmatrix}1 \\ -1\end{bmatrix}\]

\[A =\begin{bmatrix}1&2 \\ 3&1\end{bmatrix},\;\;\;B =\begin{bmatrix}1&2 \\ 0&1\end{bmatrix},\;\;\;C =\begin{bmatrix}0.5&1 \\ 0.5&2 \end{bmatrix},\;\;\;I =\begin{bmatrix}1&0 \\ 0&1\end{bmatrix}\]

  1. Calculate FIRST by hand and THEN using python:

\[a\vec{v}_1+b\vec{v}_3\]

  1. Consider \(\vec{v}_1\),\(\vec{v}_2\),and \(\vec{v}_3\), which of these vectors are linearly dependent. How do you know?

  2. Calculate FIRST by hand and THEN using python:

\[ A\cdot\vec{v}_1 \]

  1. Find the determinants of \(A\),\(B\) and \(C\). What does this tell you about these matrices if we are thinking about the size of the transformation? Do these FIRST by hand then THEN using python.

  2. In your head calculate \(I\cdot A\). Explain why this was easy enough to do in your head?

  3. Find the eigenvalues and eigenvectors of \(A\), write down the pairs - the eigenvalue with it’s associated eigenvector. See if you can sketch the eigenvectors by hand.

a = 2
b = 1/4
v1 = np.array([1,1])
v2 = np.array([2,-2])
v3 = np.array([1,-1])

A = np.array([[1,2],[3,1]])
B = np.array([[1,2],[0,1]])
C = np.array([[1/2,1],[1/2,2]])
I = np.eye(2)

#1
v = a*v1+b*v3
print(v)

#2
if np.linalg.det(np.stack((v1,v2),axis=1)) == 0:
    print('v1 is linearly dependent to v2')
    print('They are constandt multiplues of each other')
    print('The determinant is zero!')
if np.linalg.det(np.stack((v2,v3),axis=1)) == 0:
    print('v2 is linearly dependent to v3')
    print('They are constandt multiplues of each other')
    print('The determinant is zero!')
if np.linalg.det(np.stack((v3,v1),axis=1)) == 0:
    print('v3 is linearly dependent to v1')
    print('They are constandt multiplues of each other')
    print('The determinant is zero!')

#3
print(A@v1)

#4
print(np.linalg.det(A))
print('This will expand our space - we dont care about the negative')
print(np.linalg.det(B))
print('This will not change the area')
print(np.linalg.det(C))
print('This will shrink our space.')

#5
print('I is the identity so multiplying A by it just gives us back A!')

#6
eigenvalues, eigenvectors = np.linalg.eig(A)
print("EIGENVALUES")
print(eigenvalues)

print("EIGENVECTORS")
print(eigenvectors)

print(f'lambda1 = {eigenvalues[0]} and v1 = {eigenvectors[:,0]}')
print(f'lambda2 = {eigenvalues[1]} and v2 = {eigenvectors[:,1]}')
[2.25 1.75]
v2 is linearly dependent to v3
They are constandt multiplues of each other
The determinant is zero!
[3 4]
-5.000000000000001
This will expand our space - we dont care about the negative
1.0
This will not change the area
0.5
This will shrink our space.
I is the identity so multiplying A by it just gives us back A!
EIGENVALUES
[ 3.44948974 -1.44948974]
EIGENVECTORS
[[ 0.63245553 -0.63245553]
 [ 0.77459667  0.77459667]]
lambda1 = 3.4494897427831783 and v1 = [0.63245553 0.77459667]
lambda2 = -1.4494897427831779 and v2 = [-0.63245553  0.77459667]

Part 2

Solving Linear Systems - Linear Programming

The annual Great Redlands Bake-Off Bonanza was just around the corner, and two best friends, Leo and Mia, were determined to win the coveted Golden Whisk trophy. They decided to specialize: Leo was a master of fluffy Cinnamon Swirl Buns, and Mia baked the most delectable Chocolate Chip Cookies in town. The two most critical limiting factors are their time and the number of presentation platters they have.

They have a total of 10 hours available for baking. - Each batch of Cinnamon Swirl Buns takes 3 hour to prepare and bake. - Each batch of Chocolate Chip Cookies takes 0.5 hours to prepare and bake.

They have only 12 presentation platters. - Each batch of Cinnamon Swirl Buns requires 2 platters. - Each batch of Chocolate Chip Cookies requires 1 platter.

Finally, they estimated their profit: - Each batch of Cinnamon Swirl Buns would earn them a profit of \$5. - Each batch of Chocolate Chip Cookies would earn them a profit of \$3.

Leo and Mia wanted to figure out how many batches of Cinnamon Swirl Buns and Chocolate Chip Cookies they should bake to maximize their total profit

Let

\(x\) = number of Cinnamon Swirl Buns

\(y\) = number of Chocolate Chip cookies

  1. Write down the constraints
  2. Write down the function you want to maximize
  3. Plot the feasible region
  4. Solve for the intersection point using the matrix inverse.
  5. Check the points and solve for the maximum profit.
# Constraint on time 3x+0.5y < 10
# Constraint on platters 2x+y < 12
# Profit Z = 5x+3y

x = np.linspace(0,5,100)

y1 = 2*(10-3*x)
y2 = 12-2*x

plt.plot(x,y1,'r')
plt.plot(x,y2,'b')
plt.grid()
plt.xlim(0,5)
plt.ylim(0,15)
plt.show()

print('The feasible area is below these lines but above x=0 and y=0')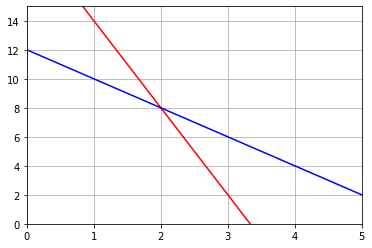

The feasible area is below these lines but above x=0 and y=0
# Solve the intersection point

A = np.array([[3,0.5],[2,1]])
b = np.array([10,12])

x = np.linalg.inv(A)@b
print(x)

print('Max Profit at either (2,8), (10/3,0), or (0,12):')
print(5*x[0]+3*x[1])
print(5*(10/3)+3*0) # Where red line intersects y=0
print(5*0+3*12) # Where blue line intersects x=0
[2. 8.]
Max Profit at either (2,8), (10/3,0), or (0,12):
34.0
16.666666666666668
36
## 36 = 5x+3y
Z = 36
x = np.linspace(0,5,100)

y1 = 2*(10-3*x)
y2 = 12-2*x

plt.plot(x,y1,'r')
plt.plot(x,y2,'b')
plt.plot(x,(Z-5*x)/3,'-k')
plt.grid()
plt.show()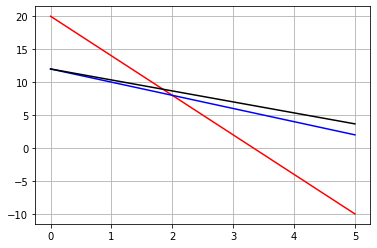

Part 3

Dimensionality Reduction:

Consider the data below with the following totally made up story:

You live in a magical dimension where crystals hold deep magic and allow the owner of the crystal great academic powers. Students who hold the magical crystals while studying have perfect retention of information and also gain a deep understanding of the applications of what they are learning. In fact, even after the crystal energy is drained, academic curiosity remains! The problem is that some crystals are not magical and instead cause an instant drain on energy. You can’t know just by looking what kind of crystal you are about to pick up. Since it is soon to be finals week we are going to set out to find only the best crystals for our academic pursuits!

  1. Read in the data and notice that there are four features and one label. What are the features and what is the label.
  2. Do a PCA analysis and project the data onto two dimensions and create a scatter plot.
  3. Report the Explained Variance Ratio and explain what it means.
  4. Now imagine that you find crystals (measured without picking them up of course) - You can load in the new crystals data. See if you can see where these new crystals land in the projected space - add them to your scatter plot. Which one would you keep? HINT You can use .transform() to run new data through your model!

  • Run the data through your standard scalar:

    scalar.transform()

  • Run the data through your PCA

    PCA.transform()
filename='https://joannabieri.com/mathdatascience/data/glowcrystal.csv'
df = pd.read_csv(filename)
df
Radiant Intensity Crystalline Volume Aura Flux Clarity Index Magical
0 2.248357 11.620420 5.846293 80.751479 0.0
1 1.930868 8.074589 15.793547 81.039345 0.0
2 2.323844 6.615390 16.572855 77.959926 0.0
3 2.761515 13.058381 11.977227 80.696761 0.0
4 1.882923 15.154998 18.387143 80.879217 0.0
... ... ... ... ... ...
95 7.765849 35.149633 72.784599 93.123297 1.0
96 7.667538 46.297199 52.622988 88.147462 1.0
97 7.542670 42.151097 53.110435 100.415489 1.0
98 9.235818 45.690035 61.378669 94.541841 1.0
99 8.283487 44.407402 67.438634 99.951265 1.0

100 rows × 5 columns

features = ['Radiant Intensity','Crystalline Volume',' Aura Flux','Clarity Index']
color_mapping = [ 'mediumturquoise' if i == 1 else "yellowgreen" for i in df['Magical']]
df['color']=color_mapping
df
Radiant Intensity Crystalline Volume Aura Flux Clarity Index Magical color
0 2.248357 11.620420 5.846293 80.751479 0.0 yellowgreen
1 1.930868 8.074589 15.793547 81.039345 0.0 yellowgreen
2 2.323844 6.615390 16.572855 77.959926 0.0 yellowgreen
3 2.761515 13.058381 11.977227 80.696761 0.0 yellowgreen
4 1.882923 15.154998 18.387143 80.879217 0.0 yellowgreen
... ... ... ... ... ... ...
95 7.765849 35.149633 72.784599 93.123297 1.0 mediumturquoise
96 7.667538 46.297199 52.622988 88.147462 1.0 mediumturquoise
97 7.542670 42.151097 53.110435 100.415489 1.0 mediumturquoise
98 9.235818 45.690035 61.378669 94.541841 1.0 mediumturquoise
99 8.283487 44.407402 67.438634 99.951265 1.0 mediumturquoise

100 rows × 6 columns

np.random.seed(42)  # for reproducibility

# Select the features - CHANGE BASED ON YOUR DATA
features = ['Radiant Intensity','Crystalline Volume',' Aura Flux','Clarity Index']
# Normalize the data
# Z-score normalization 
scalar = StandardScaler()
inputs = scalar.fit_transform(df[features]) #CHANGE BASED ON YOUR DATA

# Create the model
model = PCA(n_components=2) #CHANGE BASED ON NUMBER OF COMPONENTS YOU WANT
x_proj = model.fit_transform(inputs)

# Make a scatter plot
plt.figure(figsize=(8, 6))  # Adjust figure size as needed
# Color the plot based on malignant or not
color = df['color'].values
plt.scatter(x_proj[:,0], x_proj[:,1], c=color) #plot points
plt.xlabel("Data Projected onto 2D")
plt.axhline(0, color='black', linewidth=0.8) #draw the numberline
plt.grid(True, axis='x', linestyle='--', alpha=0.6) #add grid for x-axis
plt.show()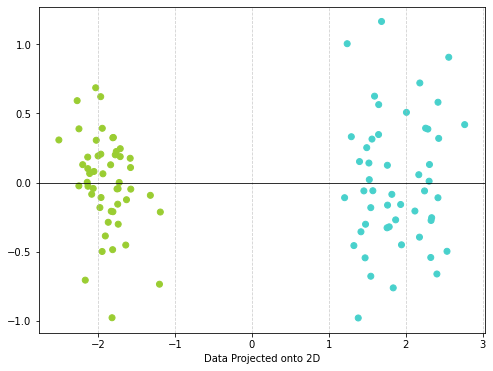

new_crystals = np.array([[2,    11.5,   5.8,     81],
                           [1.8,    15, 18.3,   90],
                           [7.5,    42, 54, 95]])

new_crystals_df = pd.DataFrame(new_crystals, columns=features)
print("\nNew Crystals Data:")
print(new_crystals_df)

new_inputs = scalar.transform(new_crystals_df[features]) 
new_x_proj = model.transform(new_inputs)
print(new_x_proj)

New Crystals Data:
   Radiant Intensity  Crystalline Volume   Aura Flux  Clarity Index
0                2.0                11.5         5.8           81.0
1                1.8                15.0        18.3           90.0
2                7.5                42.0        54.0           95.0
[[-2.02738704  0.15560347]
 [-1.19472878 -0.4876404 ]
 [ 1.50526909  0.2907625 ]]
# Make a scatter plot
plt.figure(figsize=(8, 6))  # Adjust figure size as needed
# Color the plot based on malignant or not
color = df['color'].values
plt.scatter(x_proj[:,0], x_proj[:,1], c=color) #plot points
plt.scatter(new_x_proj[:,0], new_x_proj[:,1], c='red') #plot points
plt.xlabel("Data Projected onto 2D")
plt.axhline(0, color='black', linewidth=0.8) #draw the numberline
plt.grid(True, axis='x', linestyle='--', alpha=0.6) #add grid for x-axis
plt.show()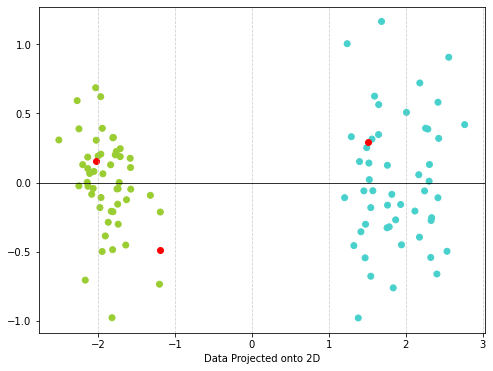

I would take the third crystal!!!